和歌山サイエンスカフェ「インフィニティ」

新シリーズの
『わかやま路上観察学』

和歌山の街で見つけた、美しいもの
面白いものをアップしていくシリーズ。

超芸術トマソンや、なにげないものを
見つけていきます。

評価は読者におまかせ。

第１弾
「とある駅で見つけたベンチ」

電線を架線するコンクリート柱の
ための気遣いと手仕事の丁寧さを感じる






  

2017年初頭のモバイルノート（ウルトラブック）な
パソコンを比較検討中。
それなりのCPUパワーと、１６GB、５１２GB（できれば１TB）のSSD
で、１．３キロくらいより軽くて、コンパクトな電源アダプターなのが
必要条件だとする。
お金を出せれば候補も増えるので、２０万円以下くらいが候補。

１．MacBookPro　１３インチ（タッチバーなし）
　　メモリを１６GB、SSDを５１２GBにカスタマイズして、
　　１７９，８００円（税別、学割適用）
　　http://www.apple.com/jp_edu_1460/shop/buy-mac/macbook-pro?product=MLL42J/A&step=config#
　　いまなら、8,500円分のApple Storeギフトカードのプレゼント付き。

　　良い点
　　・英語キーボードが選べる。
　　・Retinaディスプレイになる。
　　・タッチバーなしモデルは、コスパは良好
　　悪い点
　　・CPUがskylake。秋くらいに Kabylakeになるとも言われている。）
・type-C に対応した、SDカードリーダとHDMIソケットのアダプターを買う必要が
　　　自分の場合ある。
　　

２．東芝 dynabook V82/B (東芝ダイレクトだと VZ72/B)
Core i7 7500U で８GBの512GBのSSD(Serial ATA)
２１４、０００円（税別） （東芝ダイレクトの会員になると割引あり）
https://dynabook.com/2in1-mobile-notebook-tablet/v-series/v82b-2016-winter-model-onyx-metallic-12-5-inch-high-end-convertible-pv82bmp-nja.html

　良い点
　・国内メーカーという点
　・いま所有してるR632は、非常に良いPCだった
　・ノングレアな画面で、タッチ対応
　・CPUはKabylake
　・HDMIもVGA接続も可能なアダプター付き（電源供給も可能）

　悪い点
　・英語キーボードなし
　・メモリ８GB設定なし
　・SSDに１TB設定なし。
　・ちょっとベゼル幅が大きめ

３．HP spectre x360（パフォーマンスモデル）
　　CPUはCore i7 7500U、メモリは16GBで、1TBのSSD（NVMe接続）
　　１６１，８００円（税別、学割適用、電話申し込みの場合）
HPの学割サイト　http://jp.ext.hp.com/campaign/personal/notebooks/2017student_pc_collection/
http://jp.ext.hp.com/directplus/personal/?jumpid=ps_74m86jxecn

　良い点
　・CPUはKabylake
　・１６GBも１TBも満たす。しかも、NVMe接続
　・コストパフォーマンつ高め
　・２月２８日までに申し込むと、Office Businessが無料

　悪い点
　・やや重め（１．３ｋｇ）
　・英語キーボードなし
　・電源アダプターのコードが太め
　・HPにやや悪い印象


他にもDELL(XPS13)とかLenovo(Carbon)なども候補にあがるかも。
隠し玉はXiaomiですが、一応、法的な問題もあるので。

spectrex360とXPS13との比較動画


spectre360とMacBookPro13との比較動画

  

第２回目では、さっそくソースをアップする。

今回は、有限体積法の教科書としては、詳しい解説と、例題の丁寧な
回答が掲載されている
『数値流体力学 第2版』
の例題６．２をコード化した。

定常の移流方程式を解いている。
この例題を解いてみたのは、これから解きたい浅水流方程式に
近い形であること。つまり、速度場と密度場が未知であり、
これらを求めるためにSIMPLEアルゴリズムを適用するものであるためである。
また、断面形状も一定でなく、変化しているところも
今後の応用性が高く、参考になると思う。

Javaについては、１か月程度の知識しかなく、
静的メソッドのみの使用と、mainメソッドにほとんどの必要な処理を書いた。
初めて作ったJavaコードなので、至らないところが多い。

勉強しながら、現在はクラス等を用いたコードに修正を加えている。
また、多次元配列の初期化については、
「Arrays#fillメソッドの多次元版の一例」
を利用させていただいた。

連立方程式の解法には、トーマス法を用いている。
格子には等間隔のスタッガード格子を採用している。
また、例題の解答を直接コーディング化ではなく、最後の方に触れられている
不足緩和も係数計算の際に、組み込んでいる。

格子の数や不足緩和の係数を、いろいろ試してみたり、
質量フラックスを計算したりしてみて、有限体積法の面白さを
感じることができると思う。

（注）コードの利用による損害等は一切責任を負いません。

/*
* 有限体積法の計算
* 数値流体力学（第２版）
*
* 2017/2/11
* KZ
*
*/

package FVM;

import java.util.Arrays;

public class FvmTest007 {

public static void main(String args[]){

int nn = 5; // 圧力ポイントの数
int it_max = 200; // 最大回数
int count = 0; // 計算回数の記憶用
double r_limit = 10e-5; // 残差の制限


double m_0 = 1.0; //　初期仮定の質量フラックス
double p_0 = 10.0; // 上流端の圧力
double rho = 1.0; // 密度
double alpha = 0.7; // 不足緩和の係数 (nn,alpha)=(10,0.7),(20,0.5)
double residual = 0.0; // 残差

//double[] A_p = {0.5 ,0.4 ,0.3 ,0.2 ,0.1}; //圧力ポイントの面積
double[] A_p = new double[nn];
for(int i=0; i < nn; i++){
A_p[i] = 0.5 - (0.5-0.1)/(nn-1) * i;
}
//double[] A_u = {0.45,0.35,0.25,0.15};
double[] A_u = new double[nn-1];
for(int i=0; i < nn-1; i++){
A_u[i] = ( A_p[i] + A_p[i+1] ) / 2.0;
}

double[] x_u = new double[nn-1]; // 速度場
double[] u_star = new double[nn-1]; // 補正後の速度
double[] u_old = new double[nn-1]; // 速度の古いもの保存（残差計算用）
//double[] x_p = new double[nn]; // 圧力場
//double[] x_p = {10.0, 7.5, 5.0, 2.5, 0.0}; // 圧力場と仮定初期値
double[] x_p = new double[nn];
for(int i = 0; i < nn; i++){
x_p[i] = 10.0 - (10.0 - 0.0)/(nn-1) * i;
}
double[] p_prime = new double[nn]; //　圧力の補正値
double[] p_star = new double[nn]; // 補正後の圧力
double[] d = new double[nn-1]; // 圧力補正のパラメータ

double u_in = 2.0; // 上流端の流速（境界条件）

//方程式の係数
double F_w = 0.0;
double F_e = 0.0;
double a_W = 0.0;
double a_E = 0.0;
double a_P = 0.0;
double S_u = 0.0;

double b_prime = 0.0;

//連立方程式の係数行列
double[][] matrixA = new double[nn-1][nn-1];
double[] matrixB = new double[nn-1];


double[][] matrixC = new double[nn][nn];
double[] matrixD = new double[nn];


//配列の初期値
Arrays.fill(x_u,0.0);
Arrays.fill(u_star, 0.0);
Arrays.fill(p_prime, 0.0);
Arrays.fill(p_star, 0.0);
Arrays.fill(d, 0.0);
ArraysfillEx.fill(matrixA, 0.0); //多次元配列の初期値
Arrays.fill(matrixB, 0.0);
ArraysfillEx.fill(matrixC, 0.0); //多次元配列の初期値
Arrays.fill(matrixD, 0.0);



//速度場の初期仮定の設定
for(int i = 0; i < nn-1 ; i++){
x_u[i] = m_0 / ( rho * A_u[i] );
}

System.out.println("x_u : "+Arrays.toString(x_u)); // 行列の標準出力
System.out.println("x_p : "+Arrays.toString(x_p)); // 行列の標準出力
System.out.println("A_u : "+Arrays.toString(A_u));
System.out.println("A_p : "+Arrays.toString(A_p));



//計算の開始
for(int it = 0; it < it_max ; it++){

System.out.println("Count : " + it);

// 速度の更新（残差計算用）
for(int i = 0; i < nn-1 ; i++){
u_old[i] = x_u[i];
}
residual = 0.0; // 残差の初期化


//運動量保存則　始まり
//速度の格子点//
//格子点　1(0)
u_in = x_u[0] * (A_u[0] / A_p[0]); System.out.println("u_in : " + u_in);
F_w = rho * u_in * A_p[0]; //System.out.println(F_w);
F_e = rho * (x_u[0] + x_u[1])/2 * A_p[1]; //System.out.println(F_e);

a_W = 0.0;
a_E = 0.0;
a_P = F_e + F_w * 0.5 * Math.pow((A_u[0]/A_p[0]),2.);


S_u = (x_p[0]-x_p[1])*A_u[0] + F_w*(A_u[0]/A_p[0])*x_u[0] + (1-alpha)*a_P/alpha * x_u[0];
a_P = a_P/alpha; //不足緩和

matrixA[0][0] = a_P;
matrixA[0][1] = -1.0 * a_E;

matrixB[0] = S_u;

d[0] = A_u[0]/ a_P * alpha;//不足緩和


//格子点　2,3(1 〜 nn-3)
for(int i=1 ; i < nn-2;i++){
F_w = rho * (x_u[i-1] + x_u[i])/2 * A_p[i];
F_e = rho * (x_u[i] + x_u[i+1])/2 * A_p[i+1];
a_W = Max(F_w,0.0);
a_E = Max(0.0, -1.0*F_e);
a_P = a_W + a_E + (F_e - F_w);

S_u = (x_p[i]-x_p[i+1])*A_u[i] + (1-alpha)*a_P/alpha * x_u[i];//不足緩和
a_P = a_P/alpha; //不足緩和

matrixA[i][i-1] = -1.0 * a_W;
matrixA[i][i] = a_P;
matrixA[i][i+1] = -1.0 * a_E;

matrixB[i] = S_u;

d[i] = A_u[i]/ a_P * alpha;
}


//格子点 4(nn-2)
F_w = rho * (x_u[nn-3] + x_u[nn-2])/2 * A_p[nn-2]; //System.out.println(F_w);
//F_e = rho * (x_u[nn-2] + x_u[1])/2 * A_p[1]; //System.out.println(F_e);
if(it == 0) {
F_e = m_0; // 最初の計算だけ　要検討！！！
}else{
F_e = rho * x_u[nn-2] * A_u[nn-2];
}

a_W = F_w;
a_E = 0.0;
a_P = a_W + a_E + (F_e - F_w);

S_u = (x_p[nn-2]- x_p[nn-1])*A_u[nn-2] + (1-alpha)*a_P/alpha * x_u[nn-2];
a_P = a_P/alpha; //不足緩和

matrixA[nn-2][nn-3] = -1.0 * a_W;
matrixA[nn-2][nn-2] = a_P;

matrixB[nn-2] = S_u;

d[nn-2] = A_u[nn-2]/ a_P * alpha;



//System.out.println("matA: "+Arrays.deepToString(matrixA));
//System.out.println("matB: "+Arrays.toString(matrixB));
//System.out.println(" d : "+Arrays.toString(d));

//連立方程式を解く

u_star = thomas(nn-1,matrixA,matrixB);

System.out.println("u_star: " + Arrays.toString(u_star));

//運動量保存則　終わり

//圧力の補正式　始まり
//圧力の格子点 1,A (0)
matrixC[0][0] = -1.0;

//圧力の格子点 2から4,A (1 - nn-2)
for(int i = 1; i < nn-1 ; i++){
a_W = rho * d[i-1] * A_u[i-1];
a_E = rho * d[i] * A_u[i];
F_w = rho * u_star[i-1] * A_u[i-1];
F_e = rho * u_star[i] * A_u[i];
a_P = a_W + a_E;
b_prime = F_w - F_e;

matrixC[i][i-1] = -1.0 * a_W;
matrixC[i][i] = a_P;
matrixC[i][i+1] = -1.0 * a_E;

matrixD[i] = b_prime;
}

//圧力の格子点 5,E (nn-1)
matrixC[nn-1][nn-1] = -1.0;


//System.out.println("matC: "+Arrays.deepToString(matrixC));
//System.out.println("matD: "+Arrays.toString(matrixD));

//連立方程式を解く
p_prime = thomas(nn,matrixC,matrixD);

System.out.println("p_prime: " + Arrays.toString(p_prime));

//圧力の補正式　終わり

//圧力の補正　始り
for(int i=0;i < nn;i++){
x_p[i] = x_p[i] + alpha * p_prime[i];
}
System.out.println("calculated x_p : " + Arrays.toString(x_p));
//圧力の補正　終わり

//速度の補正　始まり
for(int i=0;i < nn-1;i++){
x_u[i] = u_star[i] + d[i] * (p_prime[i] - p_prime[i+1]);
}
System.out.println("calculated x_u : " + Arrays.toString(x_u));
//速度の補正　終わり
//格子点Aの圧力の補正
x_p[0] = p_0 - 0.5 * rho * Math.pow(x_u[0], 2.0) * Math.pow(A_u[0]/A_p[0],2.0);
System.out.println("calculated2 x_p : " + Arrays.toString(x_p));
//　終わり

// 残差の計算
for(int i = 0; i < nn-1 ; i++){
residual += Math.pow(u_old[i]-x_u[i],2.0);
}
System.out.println("residual : " + residual);

if(residual < r_limit) {
count = it;
break;
}

}

System.out.println("¥n Count: " + count);
System.out.println("x_u : " + Arrays.toString(x_u));
System.out.println("x_p : " + Arrays.toString(x_p));
System.out.println("A_u : "+Arrays.toString(A_u));
System.out.println("A_p : "+Arrays.toString(A_p));



}



//以下、メソッド

//大きい数字を返す
public static double Max(double a,double b){
if(a>b){
return a;
} else {
return b;
}
}


//トーマス法
public static double[] thomas(int n,double[][] A,double[] B){

double[] x = new double[n];

double[] g = new double[n];
double[] s = new double[n];

//配列の初期値
Arrays.fill(x,0.0);
Arrays.fill(g, 0.0);
Arrays.fill(s, 0.0);

g[0] = A[0][0];
s[0] = B[0];

for(int i = 1 ; i < n ; i++){
s[i] = B[i] - A[i][i-1]*s[i-1]/g[i-1];
g[i] = A[i][i] - A[i][i-1]*A[i-1][i]/g[i-1];
}

x[n-1] = s[n-1]/g[n-1];

for(int i = n-2 ; i >= 0; i--){
x[i] = (s[i]-A[i][i+1]*x[i+1])/g[i];
}

return x;
}
}

  

windows7ノートに
Latexをインストールした。

Texインストーラ３を利用
http://www.math.sci.hokudai.ac.jp/~abenori/soft/abtexinst.html

参考にしたサイト
http://did2memo.net/2016/04/24/easy-latex-install-windows-10-2016-04/  

ここ数ヶ月、流体の数値計算の勉強を続けている。
２次元の河床変動プログラムを作るのが、当面の最終目標。

河床変動の計算の基礎式は、
１：流体の質量保存則（連続の式）
２；流体の運動量保存則（ナビエストークス方程式）
３；流砂の連続式
４；流砂量式
である。これら４つの方程式を解くことで
流れの場を一般的には求めることができる。

これらの式は複雑に絡み合い、特に２の運動量保存則は、
非線形の方程式（移流方程式）であり、一般に解析的に解くことが
できない。
そこで、数値計算が多用される。

数値計算においては、上記の方程式を離散化して、
解く方法がとられている。

その離散化の方法の違いにより、大きく
１：　格子法
２：　粒子法
に区別される
（他に個別要素法があるが、どう分類されるのかはまだ、勉強不足）

最近は２の粒子法も注目を集めているが、
計算範囲が大きい場合や、時間スケールを長くするには、
計算パワーが必要なことから、まだまだ一般的ではない。
粒子法については
『粒子法入門 流体シミュレーションの基礎から並列計算と可視化まで C/C++ソースコード付』
が詳しくて分かりやすい。

このため、一般には１の格子法が採用される。
格子法は、さらに、
A：差分法
B：有限体積法
C；有限要素法
などに分類される。

差分法は、微分方程式をテイラー展開を利用して離散化する。
また、有限要素法は、重み付きの関数を用いて離散化する。
（有限要素法も勉強不足）
一方で、有限体積法は、コントロールボリュームと呼ばれる
有限な体積の要素に積分することで、その収支を用いて離散化する。
有限体積法では、コントロールボリュームの質量収支等を考慮するので、
質量が保存されやすいという特があり、この点が他の計算方法との違いと
言われている。

連続体としての質量の保存を重視する流体力学の数値計算では、
有限体積法が人気を集めているようである。
他の工学分野（構造力学等）では、有限要素法が一般的なようである。

以上のような理由から、有限体積法を用いて、
数値計算（数値シミュレーション）を進めていくこととした。


なお、使用言語は、
Javaを使っていくことにする（途中で変更するかもしれない）
もともと数値計算でよく用いられているFortranも使っていたが、
Androidアプリ開発のため、Javaを勉強し始めたことと、
オブジェクト指向を理解するためにも、Javaをプログラミング言語として
学んでいくことは、今後に役立つと考えたためである。


有限体積法の勉強に用いた参考文献を以下に示す。








  

GMT5.3.1を使い、国土地理院の基盤地図情報サービスの
１０mメッシュのDEMから、地形の陰影図や鳥瞰図を作る。

まずはデータのダウンロード
http://www.gsi.go.jp/kiban/
（今回は紀伊半島の一部のデータを利用）

登録してダウンロードし解凍してできる
FG-GML-5035-37-dem10b-20161001.xml
を利用します。

GMTで扱えるgrd形式に変換する必要がある。
grd形式に変換するスクリプトを
産業技術研究所の野田さんが公開されているので
利用させていただく。ありがとうございます。
https://staff.aist.go.jp/a.noda/programs/jpgis2grd/jpgis2grd.html

このスクリプトを動かすとgrd形式に変換できるが
一部環境に合わせて変更する。
（commandを「gmt xyz2grd」とか出来上がるファイル名などの変数を）

$ perl jpgis2grd.pl
を実行
しかし、エラーで止まる。
途中のどこかに３列目の数値がないところがあるようだ。
（今回は 843751行目）

このスクリプトのglobal optionに
my $outfile2 = "out2.xyz"
を追記。

grdに変換するあたりを

print STDOUT "Making a grd file.\n";
# my $command="gmt xyz2grd $outfile -R$xmin/$xmax/$ymin/$ymax -I$xint/$yint -G$grdfile -N-9999 -Dlongitude/latitude/height/1/0/$opts{title}/$opts{remark} ";
my $command_sed="sed -e '843751d' $outfile > $outfile2";
my $command="gmt xyz2grd $outfile2 -R$xmin/$xmax/$ymin/$ymax -I$xint/$yint -G$grdfile -di-9999 -Dlongitude/latitude/height/1/0/$opts{title}/$opts{remark} ";
if ($opts{verbose}) { print STDERR "Running \"$command\"\n"; };
system("$command_sed");
system("$command");
system("gmt grdinfo $grdfile");

と一部修正。
（perlに詳しくないので、あんまりいいやり方ではなさそうですが）

再度、
$ perl jpgis2grd.pl -v -n
を実行
（実行状況や中間ファイルを残すのに　-v -nオプションをつけた）

すると、out.grdファイルができるので
とりあえず、これを
FG-GML-5035-37-dem10b-20161001.grd
と名前を変更。

次はgmtで陰影図を描く
以下のスクリプトで
#!/bin/bash
#
# DEM10mメッシュのgrdファイルから陰影図を作る。
# 2016/12/12
#
# perl jpgis2grd.pl で出力される範囲をコピー
# xmin=135.87500000, xmax=136.00000000, ymin=33.58333333, ymax=33.66666667

grd_file=FG-GML-5035-37-dem10b-20161001.grd
shade_file=5035-37.shade
eps_file=5035-37_inei.eps
cpt_file=color.cpt
ctb=-1000/1000/50 #color table min/max/interval
region=135.875/136.00/33.5833333/33.6666667

gmt makecpt -Cglobe -T$ctb -Z > $cpt_file

gmt gmtset FORMAT_GEO_MAP D

gmt grdgradient $grd_file -A90 -G$shade_file -Ne0.6 -V
gmt grdimage $grd_file -R$region -JM15 -C$cpt_file -I$shade_file -X4 -Y4 -K > $eps_file
gmt psscale -D7.5/-1/12/0.3h -C$cpt_file -Ba200f100:"altitude(m)": -I -V -K -O >> $eps_file
gmt psbasemap -R$region -JM15 -Ba0.05f0.025g0.01 -O -V >> $eps_file

こんな図ができる



次は鳥瞰図
#!/bin/bash
#
# DEM10mメッシュのgrdファイルから陰影図を作る。
# 2016/12/12
#
# perl jpgis2grd.pl で出力される範囲をコピー
# xmin=135.87500000, xmax=136.00000000, ymin=33.58333333, ymax=33.66666667

grd_file=FG-GML-5035-37-dem10b-20161001.grd
shade_file=5035-37.shade
d3_file=5035-37_3d.eps
cpt_file=color.cpt
ctb=-1000/1000/50 #color table min/max/interval
region=135.875/136.00/33.5833333/33.6666667
boundary_cap=wSnEZ
gmt makecpt -Cglobe -T$ctb -Z > $cpt_file
gmt gmtset FORMAT_GEO_MAP D
gmt grdgradient $grd_file -A90 -G$shade_file -Ne0.6 -V
gmt grdview $grd_file -Jm130 -Jz0.002 -C$cpt_file -I$shade_file -p150/25 -Ba0.05f0.025g0.01 -Bza400 -B$boundary_cap -Qi300 -N0+ggray -V > $d3_file

を実行すると、鳥瞰図ができる。



角度とかは適宜設定する。

  

久しぶりに綺麗なグラフとかを描きたくて
GMTを触ってみた

バージョンが５に上がっていて、いろいろ
変わったところが多い。
インストールはubuntuの場合cmakeでしたり
するようになっていたり。

プログラミングもコマンドからモジュールという
概念に変わっているようだ。
例えば
gmt pscoast ほにゃらら
と入力する。

より日本語の情報が少ないので
できたことはアップしてみる。

今回は紀伊半島周辺の海岸線図に
県境と、距離スケールと方位を示す矢印を追記する。
矢印、というかベクトルを書くのに手間取った。

gmtのバージョン5以降は
インストールできているとして、
県境のデータをダウンロード。
こちらを参考に
http://www.geocities.jp/ne_o_t/otenki.htm

後は、観測地点なんかも記載できたらいいので、
std_name.dataと名付けたファイル
　　NachiRiver 33.668 135.904
と、std＿point.dataと名付けたファイル
　　135.904 33.668 LM 0.0 12p,Helvetica,255/0/0 NachiRiver
を用意。

今回はmacで作業してるので、あんまりgmtのファイルが
どこにあるかわからないので、shareと名付けたファイルに
県境のデータ ken.txtを置いて、以下のようなシェルスクリプトを書いて実行。

#!/bin/bash
# kenzakai_wakayama.sh

rangeSW=134.5/136.5/33/35
scale=M10c
afg=a1f0.5g0
ruler=136/33.3/33.2/50k
pen1=0.6p,black #[width,color]
pen2=0.4p,50
g_color=200
s_color=255

point_data=stn_point.dat
name_data=stn_name.dat

fig=Wakayama.eps

gmt gmtset FORMAT_GEO_MAP +DF
gmt set MAP_VECTOR_SHAPE 0

gmt psbasemap -J$scale -R$rangeSW -B$afg -X3c -Y3c -P -V -K > $fig
gmt pscoast -J -R -B$afg -Lf145/30/35/500 -Dh -P -W$pen1 -G$g_color -S$s_color -L$ruler -V -O -K >> $fig
gmt psxy ../share/ken.txt -J -R -W$pen2 -O -K >> $fig
gmt psxy $point_data -i2,1 -J -R -Sc0.2c -G255/0/0 -V -O -K >> $fig #地点の位置
gmt pstext $name_data -J -R$rangeSW -D0.5/0 -F+j+a+f -O -K >> $fig #地点の名前 -Dはシフト

#方向矢印の記述
#矢印
gmt psxy -R -J -SV0.4+s+e+a45 -W1 -G0 -O -K << EOF >> $fig #片矢印
135,33.3,135,33.65 #始点、終点
EOF
#横棒
gmt psxy -R -J -SV0.5+s -W0.8 -G0 -O -K << EOF >> $fig #線分を引く
134.93,33.45,135.07,33.45 #始点、終点
EOF
#Nの文字
gmt pstext -R$rangeSW -J -D0/0.1 -F+j+a+f -O << EOF >> $fig
135 33.65 BC 0.0 12p,Helvetica,black N
EOF

#白抜きのpngの作成
#convert -density 100 test2.ps test2.png
# mogrify -trim -density 300 -bordercolor 'transparent' -border 10x10 -format png *.eps
#mogrify -trim -density 300x300 -transparent white -format png $fig


以上。
最後でコメントアウトしてるけど、
imagemagicを使って、白のところを透明にしたpngファイルも
作成できるようにしている。

こんな図ができると思う。（クリックして拡大）


ベクトルを書くのに、psxyの-SVオプションが結構戸惑った。
WANtaroHP (Programing on Mac)さん
http://kbtkt.web.fc2.com/sub_0_gmt5.html
を参考にさせてもらった。ありがとうございます。  

礫の移動を表示するため
QGISに、
WKTのテキストデータを
レイヤー追加して、ラインを引いた。

矢印表示にできるように
ラインのプロパティを以下のように設定。



こんな感じです。（赤の矢印）


画像をクリックしたら、大きく表示されます。  

３年ほど使ってるMac mini(Late2012)の
ハードディスクをSSDに交換してみました。
ずっと思ってたけど、ちょっと難しく思っていたので。

このために買ったのは、

と、
交換で出てくるHDDのための外付けケース

と、
ちょっと特殊なドライバーが必要だということで


SSDが値上がり気味ってことなので、
慌てて買いました。

件のMacmini

一年ほど前にメモリは８GBに交換済み。

裏返すと

黒い蓋をヒネって開ける。


購入したドライバーでビスを外して、
ごそごそとファンを外す。




金属の金網みたいものを外す。この時
wifiのアンテナ線も外します。


すると、黒いカバーに覆われたHDDが見える。
ごそごそと引き抜く。
自分のMacminiは、下側（ちゃんと置くと）にあったので、取りやすい方だった。
上側にあるものもあるらしい。そうなると、作業がさらに増えるみたい。



HDDについてる部品を外して、SSDに装着して、
手順を遡って、元に戻すだけ。


でも、wifiのアンテナの接続部分とか、
fanの電源端子が小さくて、つけるのは結構手間取った。
ピンセットがあると便利。

SSDには予めSierraを外付けのHDDケースを使って、
インストールおいたので、すぐに起動できた。
MacはOSを簡単にダウンロードして、外付け
のドライブにインストールできるのがすごいな。

この交換作業は色々ネットに情報があるので、
今更ですが。
Mac miniはLate2012に根強い人気があるらしい。  

防災ジオツアーが
１２月１１日に開催されます。

時間は１０時から１５時３０分の予定です。
お弁当とお茶代込みの１、３００円です。

那智勝浦町にある、土砂災害啓発センターを出発して、
土砂災害の現場や砂防ダムの工事現場、
ジオサイトの「那智の滝」を巡るコースです。

申し込みは、和歌山大学災害科学教育研究センターまで。
bousai@center.wakayama-u.ac.jp

主催：和歌山大学災害科学教育研究センター、国土交通省近畿地方整備局

詳しくは、下記のフライヤーをご参照ください。
クリックすると大きく表示されます



  

働き出して、水理学ってものが
あるのを知っても、なかなか良くわからなかったのですが、
昨年くらいから、腰を据えて勉強をはじめました。

初学者向けに、寒地土木研究所さんの
「現場の水理学」という貴重な資料があるのです。
http://river.ceri.go.jp/contents/tool/suirigaku.html

こちらに、不等流計算など初歩的なところから
のプログラムコードも掲載されています。
言語はfortranです。

でも、それをそのまま打ち込んでも、
動かなかったりしたので、
ほとんどそのままですが、
fortran90の勉強も兼ねて、自分で
ソースコードを作ってみました。

ということで、たまにそのコードを掲載させて
もらいたいと思います。
プログラミングにあたり、参考にした本は、

です。

演習問題３の１階のニュートン法によるもののソース

program newton
implicit none
integer i,j
integer,parameter ::nn=10
double precision q,n,ep,g
double precision aa,bb,cc
double precision fh,f1,dh,hhh
double precision d(nn),dl(nn),z(nn),b(nn),sh(nn),hh(nn)

d=(/ 0d0,500d0,1000d0,1200d0,1800d0,2100d0,2500d0,3000d0,3300d0,3800d0 /)
z=(/ 0d0,.5d0,.9d0,.8d0,2.0d0,2.3d0,3.0d0,3.0d0,3.5d0,4.0d0 /)
b=(/ 300d0,320d0,280d0,250d0,300d0,300d0,320d0,350d0,300d0,250d0 /)


do i=2,nn
dl(i)=d(i)-d(i-1)
enddo

q=1500d0
n=0.025d0
sh(1)=2.5d0
hh(1)=sh(1)+z(1)
ep=1d-3
g=9.8d0

do j=1,nn
if(j==1) then
write(*,*) j,d(j),dl(j),b(j),z(j),sh(j),hh(j)
cycle
endif

hhh=sh(j-1)

aa=q*q/(2*g*b(j)*b(j))
bb=-q*q*n*n*dl(j)/(2*b(j)*b(j))
cc=z(j)-(z(j-1)+sh(j-1)+q*q/(2*g*b(j-1)*b(j-1)*sh(j-1)*sh(j-1))+&
q*q*n*n*dl(j)/(2d0*b(j-1)*b(j-1)*sh(j-1)**(10d0/3d0)))

10fh=hhh+aa/(hhh**2d0)+bb/(hhh**(10d0/3d0))+cc
f1=1-2d0*aa/(hhh**3d0)-10d0*bb/(3d0*hhh**(13d0/3d0))
dh=-fh/f1
if(abs(fh) < ep ) then
sh(j)=hhh
hh(j)=sh(j)+z(j)
write(*,*) j,d(j),dl(j),b(j),z(j),sh(j),hh(j)
cycle
else
hhh=hhh+dh
goto 10
endif

enddo

end program newton  

３年ぶりにスマホを買い替えました。
Nexus5からの買い替えで、
Asusのzenfone3(ZE520KL)
にしました。


電話はガラケーなので、
スマホはocnのモバイルワン（月約１０００円コース）
の通信線専用です。
simフリー版しか興味ないところです。
microSDも入れたままなので、
DSDSにも興味はないです。

なるべくコスパがいいものをってことで
zenfone3がmotoGplusと悩みましたが、
後者は電子コンパスなしってことで諦めました。

並行輸入したら安いみたいですが、
あんまり文句を言うところがないのは嫌なので
適技の問題もあるかもしれないので、
NTTXstoreで購入。
同時に、モバイルoneも買い替えました。

いろいろレビューはあるので、そちらを見てもらったら
いいですが、
かなり満足です。
指紋認証もとてもスムーズです。

ただ、lightroomモバイルを使っての
raw撮影（dng撮影）は一応できますが、
カラーマップがだめらしくて、使い物になりません。

あと、android6でありながら、
マルチユーザー（マルチアカウント）が使えません。
これは結構いたかった。

でも、その他は、十分だと思います。

USBのtypeCなので、
変換コネクタ

保護フィルム

ケース

も買いました。



  

河川シュミレーションソフトのiRICを
ひさしぶりに動かしてみました。
http://i-ric.org/ja/

まだあまり慣れてないので、
河床変動も計算できるＮａｙｓ２ＤＨソルバーを
チュートリアルで練習してみた。

ものの数時間で基本的なところは分かるみたい。
面白いですよ。

河の形を与えて、上流からの流量とかを
設定するだけ。





１１月２６日の和歌山サイエンスカフェはまだまだ
参加者募集中です！！

よろしくお願いします。
詳しくは以下のリンクを！
http://wscinfinity.ikora.tv/e1234831.html  

日時：２０１６年１１月２６日（土）
　　　１３：００受付
　　　１３：３０から１５：００
ゲスト：宮本尚樹さん
　　　　大阪府立大学理学系研究科　生物科学専攻
　　　　生命化学分野　藤井郁雄研究室
　　　　博士課程教育リーディングプログラム（SiMS）
　　　　博士後期課程
場所：水辺座
　　　　和歌山市元博労町５３
定員：１５名程度
申込：メールにて　wsc.infinity@gmail.com
参加費：１０００円
　　　（１ドリンク＋１品）
　　　ドリンクメニュー
　　　　　アルコール：日本酒、ビール、果実酒（梅酒、柚子酒、桃酒）
　　　　　ソフトドリンク：伊藤園のみかんしぼり、はっさくしぼり
　　　　　　　　　　　　（１００％ピュアジュース。素材のそのままの
　　　　　　　　　　　　　甘さと美味しさが魅力）
主催：和歌山サイエンスカフェ　インフィニティ

注意事項：運転される方、未成年者の飲酒はお断りします。


上の画像をクリックすると大きく表示されます。
  

QGISでラインを引くにはWKTという形で記述した
CSVファイルを用意するとよい。

こんな感じのファイル

ID WKT hoge
1 LINESTRING(-9634.725 -260090.329,-9634.715 -260090.363) hogehoge
2 LINESTRING(-9637.913 -260090.775,-9637.916 -260090.777) hogehogehoge

これを
「レイヤー」
「レイヤーの追加」
「デリミテッドテキストファイルの追加」
を選び、
WKT(Well Known Text)形式を選択する。  

気象庁が出している土壌雨量指数を
読み込むプログラムをC#の勉強を
兼ねて作ってみた。

全然、わからなかったので、
「ロケッこが行く」のブログ
http://blog.syo-ko.com/?eid=1228
を大変参考にさせてもらった。
ありがとうございます。

grib2形式のバイナリーファイルでできている。
データ部はランレングスという形で表現されていて
この読み方に結構時間を取られた。

ちなみに、気象庁が出している技術資料は
http://www.data.jma.go.jp/add/suishin/jyouhou/pdf/302.pdf
から取れる。
でも、タンクの数が違ったり、まだまだ謎が多い。
自分の理解不足か、よくわからない。

ちょっとづつC#の勉強しながらなので、
全然クラスの使い方とか、ファイルの読み込み方とか
統一とれてない上に、動作確認のためのコンソールへの
出力とかをコメントアウトのまま残してる。

ネットで検索すると、土壌雨量指数の読み込みプログラムが、
異常な値段で売られてたりするので、
少しでも役に立てればうれしい。

ただ、実行は自己責任でお願いします。

できたテキストファイルをRで描画すると

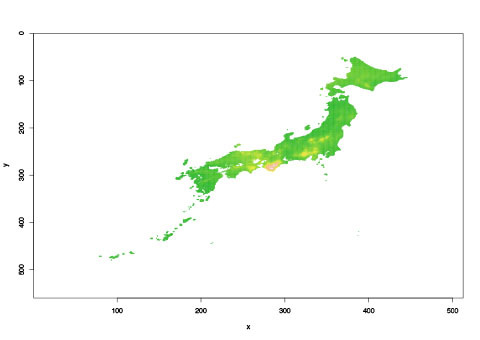
それっぽいので、たぶんうまくいけてる。

で、ソースは以下のとおり。

using System;
using System.IO;

class DojoUryouANAL
{


static void Main()
{

int FileYear = 2011;　//入力年の指定
int[] nMonth = new int[] { 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
nMonth[2 - 1] = 28 + (1 / (FileYear % 4 + 1)) * (1 - 1 / (FileYear % 100 + 1)) + (1 / (FileYear % 400 + 1)); //２月のうるう年判別

int nCount = 0;
int FileMonth = 1;
int FileDay = 1;
int FileHour = 0;
int FileMinute = 0;
int FileSecond = 0;

string InputFile1 = "InputFiles¥¥Z__C_RJTD_";
string InputFIle2 = "_SRF_GPV_Gll5km_P-swi_ANAL_grib2.bin";

string[] InputFileNameList = new string[18000];

while (FileMonth < 13)
{
while (FileDay < nMonth[FileMonth - 1] + 1)
{
while (FileHour < 24)
{
for (int minIndex = 0; minIndex < 2; minIndex++)
{
if (minIndex == 0)
{
FileMinute = 0;
InputFileNameList[nCount] = InputFile1 + FileYear.ToString("D4") + FileMonth.ToString("D2") + FileDay.ToString("D2") + FileHour.ToString("D2") + FileMinute.ToString("D2") + FileSecond.ToString("D2") + InputFIle2;
//Console.WriteLine("InputFile = " + InputFileName);
// Console.WriteLine("Year={0},Month={1},Day={2},Hour={3},Minute={4},Second={5}", Year, Month, Day, Hour, Minute, Second);
nCount++;
}
else
{
FileMinute = 30;
InputFileNameList[nCount] = InputFile1 + FileYear.ToString("D4") + FileMonth.ToString("D2") + FileDay.ToString("D2") + FileHour.ToString("D2") + FileMinute.ToString("D2") + FileSecond.ToString("D2") + InputFIle2;
//Console.WriteLine("InputFile = " + InputFileName);
//Console.WriteLine("Year={0},Month={1},Day={2},Hour={3},Minute={4},Second={5}", Year, Month, Day, Hour, Minute, Second);
nCount++;
}
}
FileHour++;
}
FileHour = 0;
FileDay++;
}

FileDay = 1;

FileMonth++;

}


for (int sCount = 0; sCount < nCount; sCount++)
{

string InputFileName = InputFileNameList[sCount];
//string InputFileName = "Z__C_RJTD_20110903170000_SRF_GPV_Gll5km_P-swi_ANAL_grib2.bin";
//string OutputFileName = "output.txt";
string FileHeadS = InputFileName.Substring(11, 10);
string FileYearS = InputFileName.Substring(21, 4);
string FileMonthS = InputFileName.Substring(25, 2);
string FileDayS = InputFileName.Substring(27, 2);
string FileHourS = InputFileName.Substring(29, 2);
string FileMinuteS = InputFileName.Substring(31, 2);
string FileSecondS = InputFileName.Substring(33, 2);


//string OutputFileName = "Dojosisu_ANAL_" + FileYearS + FileMonthS + FileDayS + FileHourS + FileMinuteS + ".txt";
//Console.WriteLine("OutputFileName = " + OutputFileName);

FileStream dataIN; //入力データファイル
StreamWriter fstr_out; //出力データファイル

//ファイルの読み込み（はじめ）
try
{
dataIN = new FileStream(InputFileName, FileMode.Open, FileAccess.Read);
}
catch (IOException exc)
{
Console.WriteLine(exc.Message);
return;
}

int fileSize = (int)dataIN.Length; //オクテット数
byte[] rByte = new byte[fileSize]; //rByte 全オクテットの保持配列

Console.WriteLine("File Size: " + fileSize);

int readSize;
int remain = fileSize;
int bufPos = 0; //読み込み開始ポイント

while (remain > 0)
{
readSize = dataIN.Read(rByte, bufPos, Math.Min(1, remain));

bufPos += readSize;
remain -= readSize;
}
//ファイルの読み込み（終わり）


//ファイルを閉じる。
dataIN.Dispose();




//////解釈の始まり//////
//１〜４オクテット
// for (int i = 0;i < 4; i++){
// Console.Write((char)rByte[i]+",");
// }

//９〜１６オクテット
// long rValue = ByteToInt(rByte, 8, 8);
long rValue = ByteToSingedInt(rByte, 8, 8);
Console.Write(rValue + ",");



Console.WriteLine();
Console.WriteLine("第１節");
//第１節１〜４オクテット ※節の長さ
rValue = ByteToSingedInt(rByte, 16 + 1 - 1, 4);
Console.WriteLine(rValue);
int lenFirstchp = (int)rValue;
//第１節５オクテット
rValue = ByteToSingedInt(rByte, 16 + 5 - 1, 1);
Console.WriteLine(rValue);
//第１節６〜７オクテット
rValue = ByteToSingedInt(rByte, 16 + 6 - 1, 2);
Console.WriteLine(rValue);
//第１節１３〜１４オクテット
rValue = ByteToSingedInt(rByte, 16 + 13 - 1, 2);
Console.WriteLine(rValue);
//第１節１５オクテット
rValue = ByteToSingedInt(rByte, 16 + 15 - 1, 1);
Console.WriteLine(rValue);
//第１節16オクテット
rValue = ByteToSingedInt(rByte, 16 + 16 - 1, 1);
Console.WriteLine(rValue);
//第１節17オクテット
rValue = ByteToSingedInt(rByte, 16 + 17 - 1, 1);
Console.WriteLine(rValue);
//第１節18オクテット
rValue = ByteToSingedInt(rByte, 16 + 18 - 1, 1);
Console.WriteLine(rValue);
//第１節19オクテット
rValue = ByteToSingedInt(rByte, 16 + 19 - 1, 1);
Console.WriteLine(rValue);
//第１節２０オクテット
rValue = ByteToSingedInt(rByte, 16 + 20 - 1, 1);
Console.WriteLine(rValue);


Console.WriteLine();
Console.WriteLine("第３節");

//第３節１〜４オクテット　※節の長さ
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 1 - 1, 4);
Console.WriteLine(rValue);
int lenThirdchp = (int)rValue;
//第３節５オクテット　※節番号
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 5 - 1, 4);
Console.WriteLine(rValue);
//第３節３１〜３４オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 31 - 1, 4);
Console.WriteLine(rValue);
//第３節３５〜３８オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 35 - 1, 4);
Console.WriteLine(rValue);
//第３節４７〜５０オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 47 - 1, 4);
Console.WriteLine(rValue / 1000000.0);
//第３節５１〜５４オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 51 - 1, 4);
Console.WriteLine(rValue / 1000000.0);
//第３節５６〜５９オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 56 - 1, 4);
Console.WriteLine(rValue / 1000000.0);
//第３節６０〜６３オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 60 - 1, 4);
Console.WriteLine(rValue / 1000000.0);
//第３節６４〜６７オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 64 - 1, 4);
Console.WriteLine(rValue / 1000000.0);
//第３節６８〜７１オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + 68 - 1, 4);
Console.WriteLine(rValue / 1000000.0);



int lenNow = 0;

for (int NumTank = 0; NumTank < 4; NumTank++)
{



Console.WriteLine();
Console.WriteLine("第４節");



//第４節１〜４オクテット　※節の長さ
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 1 - 1, 4);
Console.WriteLine(rValue);
int lenForthchp = (int)rValue;

//第４節5オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 5 - 1, 1);
Console.WriteLine(rValue);

Console.WriteLine();
Console.WriteLine("第５節");

//第５節１〜４オクテット　※節の長さ
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 1 - 1, 4);
Console.WriteLine(rValue);
int lenFivechp = (int)rValue;

//第５節５オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 5 - 1, 1);
Console.WriteLine(rValue);
//第５節６−９オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 6 - 1, 4);
Console.WriteLine(rValue);

//第５節１０−１１オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 10 - 1, 2);
Console.WriteLine(rValue);

//第５節１２オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 12 - 1, 1);
Console.WriteLine("nbit: " + rValue);
int nbit = (int)rValue;

//第５節１３−１４オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 13 - 1, 2);
Console.WriteLine("maxv: " + rValue);
int maxv = (int)rValue;

//第５節１５−１６オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 15 - 1, 2);
Console.WriteLine("max_M: " + rValue);
int max_M = (int)rValue;

//第５節１７オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 17 - 1, 1);
Console.WriteLine(rValue);

int[] LevelValue = new int[max_M + 1];
for (int level = 1; level < max_M + 1; level++)
{
//第５節１８−オクテット レベルの対応値
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenNow + 18 + (level - 1) * 2 - 1, 2);
LevelValue[level] = (int)rValue / 10;
Console.WriteLine("level: " + level + " Value: " + rValue);
Console.WriteLine("level: " + level + " LevelValue " + LevelValue[level]);
}
LevelValue[0] = 9999; ///欠測地

Console.WriteLine();
Console.WriteLine("第６節");


//第６節１−４オクテット ※節の長さ
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenNow + 1 - 1, 4);
Console.WriteLine(rValue);
int lenSixchp = (int)rValue;

//第６節５オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenNow + 5 - 1, 1);
Console.WriteLine(rValue);
//第６節６オクテット
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenNow + 6 - 1, 1);
Console.WriteLine(rValue);


Console.WriteLine();
Console.WriteLine("第７節");


//第７節１−４オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenSixchp + lenNow + 1 - 1, 4);
Console.WriteLine("length of this chapter: " + rValue);
int n_data = (int)rValue - 6 + 1;
int lenSevenchp = (int)rValue;

//第７節５オクテット
rValue = ByteToSingedInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenSixchp + lenNow + 5 - 1, 1);
Console.WriteLine("number of chapter: " + rValue);



//出力ファイル名の操作
string OutputFileName = "OutputFIles¥¥Dojosisu_ANAL_" + "TANK" + NumTank.ToString() + "_" + FileYearS + FileMonthS + FileDayS + FileHourS + FileMinuteS + "UTC.txt";
Console.WriteLine("OutputFileName = " + OutputFileName);


int j;
int p = -1, m = 1, n = 0, k = 0;
int v = 0;
int l = ipow(2, nbit) - 1 - maxv;

// n_data = 30;

try
{
fstr_out = new StreamWriter(OutputFileName); //土壌雨量指数の出力ファイル
}
catch (IOException exc)
{
Console.WriteLine(exc.Message);
return;
}

for (int iRun = 1; iRun < n_data + 1; iRun++)
{
// Console.WriteLine("iRun: " + iRun);

//第７節６−オクテット
// rValue = ByteToSingedInt(rByte, 16 + 21 + 72 + 58 + lenFivechp + 6 + iRun + 5 - 1, 1);
// Console.WriteLine("iRun: " + iRun + " Value: " + rValue);
// Console.WriteLine("iRun: " + iRun + " Value: " + rByte[16 + 21 + 72 + 58 + lenFivechp + 6 + iRun + 5 - 1]);
// Console.WriteLine("iRun: " + iRun + " Value: " + rByte[16 + 21 + 72 + 82 + lenFivechp + 6 + iRun + 5 - 1].ToString("X"));

v = (int)ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenForthchp + lenFivechp + lenSixchp + lenNow + iRun + 5 - 1, 1);
// Console.Write(v + ",");
if (v <= maxv)
{
if (p >= 0)
{
// Console.WriteLine(" ,m: " + m);

for (j = 0; j < m; j++)
{
k++;
// Console.Write(p+" , ");
try
{
fstr_out.Write(LevelValue[p] + " , ");
}
catch (IOException exc)
{
Console.WriteLine(exc.Message);
break;
}
}
// Console.WriteLine("p: " + p + " ,m: " + m );
p = v;
m = 1;
n = 0;
}
p = v;
m = 1;
n = 0;

}
else
{
m += ipow(l, n) * (v - maxv - 1);
// Console.WriteLine(ipow(l, n) * (v - maxv - 1)+","+m);
n++;
}

}

for (j = 0; j < m; j++)
{
k++;
if (k != 286720)
{
// Console.Write(p);
try
{
fstr_out.Write(LevelValue[p] + " , ");
}
catch (IOException exc)
{
Console.WriteLine(exc.Message);
break;
}
}
else
{
// Console.Write(p+" , ");
try
{
fstr_out.Write(LevelValue[p] + " ");
}
catch (IOException exc)
{
Console.WriteLine(exc.Message);
break;
}
}
}
Console.WriteLine("lenNow:" + lenNow);
lenNow += lenForthchp + lenFivechp + lenSixchp + lenSevenchp;
Console.WriteLine("lenNow:" + lenNow);
fstr_out.Close();
Console.WriteLine("k: " + k); //286,720=512x560

}

//第８節１−４オクテット ※-1
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 0 - 1, 1);
Console.WriteLine("¥n -1");
Console.WriteLine("Message: " + rValue);


//第８節１−４オクテット ※1
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 1 - 1, 1);
Console.WriteLine("¥nEighth Chapter 1");
Console.WriteLine("Message: " + rValue);

//第８節１−４オクテット ※2
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 2 - 1, 1);
Console.WriteLine("¥nEighth Chapter 2");
Console.WriteLine("Message: " + rValue);

//第８節１−４オクテット ※3
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 3 - 1, 1);
Console.WriteLine("¥nEighth Chapter 3");
Console.WriteLine("Message: " + rValue);

//第８節１−４オクテット ※4
rValue = ByteToInt(rByte, 16 + lenFirstchp + lenThirdchp + lenNow + 4 - 1, 1);
Console.WriteLine("¥nEighth Chapter 4");
Console.WriteLine("Message: " + rValue);

}
}
//Mainメソッド　終了


//整数の累乗を計算するメソッド
static int ipow(int i, int j)
{
int k, l;
for (k = 0, l = 1; k < j; k++) l *= i;
return (l);
}


//バイトを、整数に変換するメソッド
static long ByteToInt(byte[] source, int Start, int Length)
{
long rVal = 0;
int intB;
int intE = Start + Length;

for (intB = Start; intB < intE; intB++)
{
rVal *= 256;
rVal += Convert.ToInt64(source[intB]);

//Console.WriteLine("intB: " + intB + " ,souce: " + Convert.ToInt64(source[intB]) + " ,rval: " + rVal);
}

return rVal;

}


//バイトを、符号付き整数に変換するメソッド
static long ByteToSingedInt(byte[] source, int Start, int Length)
{
long rVal = 0;
int intB;
int intE = Start + Length;
bool bSng = true;

//先頭オクテットの確認
if ((source[Start] & 0x80) == 0x80)
{
// Console.WriteLine("負数である");
bSng = true;
source[Start] = (byte)(source[Start] & 0x7F);
}
else
{
bSng = false;
// Console.WriteLine("正数である");
}


for (intB = Start; intB < intE; intB++)
{
rVal *= 256;
rVal += Convert.ToInt64(source[intB]);

//Console.WriteLine("intB: " + intB + " ,souce: " + Convert.ToInt64(source[intB]) + " ,rval: " + rVal);

}

if (bSng == true)
{
rVal *= -1;
}

return rVal;

}


}

  

和歌山県土砂災害啓発センター（和歌山県那智勝浦町市野々３０２７−６）
にて、
『ワダイノカフェ（防災カフェ）』が
開催されます。

日時：９月１０日（土）１４：００〜１５：３０
講師：本塚智貴（人と防災未来センター　研究員）

詳しくは
http://nankikumanogeo.jp/2016/08/23/2222/
をご参照ください。


  

今日から「まいにちスペイン語」を
開始しました。NHKのラジオ講座です。

放送は朝の７時１５分から３０分
もしくはお昼の２時４５分から３時です。

４年前に一度半年間聞いていましたが、
それっきりで、今度お世話になる研究室に
スペイン語圏の方がいらっしゃるってことで、
これはチャンスだと学び直すことにしました。

英語は、学校教育で読み書きから入りましたが、
スペイン語は、耳としゃべりで学習してみたいと思ってます。
スペイン語はなんだか陽気で、鬱な気分も吹っ飛び感じで
たのしいですよぉー！

学生時代はロシア語、ドイツ語もかじりましたが、中途半端だったので、
スペイン語を選んでみました。



kidle本だと、かなり安く手に入るみたいです。
  

４月から京都大学大学院の博士後期課程に進学します。
社会人特別選抜制度というものがあり、
社会人をしながら、博士号取得に向けての
研究ができる制度です。これを活用しての進学です。

近年は、大学院、特にいわゆる博士課程に進学する
方が少なくなっているそうです。
一方で、社会人しながら、学位（博士号）取得したいと
いう方も増えてると思います。
そのような流れで、京都大学大学院も
このような制度を整備している研究科が増えているようです。

私は理学研究科で修士号を取得して、社会人になりました。
１年前から仕事で研究活動をしている一環で
農学研究科の博士後期課程に進学することを決意しました。

こういう道もあるんだな、と改めて思いつつ、
似たような境遇にある方に役立てればと、
そういう情報も追々提供できたらと思っています。

気になる入学試験ですが、農学研究科の場合、
試験は、英語と口頭試問のみでした。
英語は２時間で、英文和訳中心でした。
ある程度、英文が読めれば、それほど難しくは
ないと思います。


口頭試問では、
研究計画の概要と
修士時代の研究内容を聞かれました。


ちなみに、
授業料も、入学金も一般の国立大学生と同じです。
高いと考えるか、妥当と考えるのか、
それぞれだと思います。
久しぶりの研究生活を学びながら
楽しみたいと思ってます。


そのうち、サイエンスカフェででも、お会いできれば・・・  

和歌山大学や近畿地方整備局が主催の「防災ジオツアー」に
参加してきました。

平成２３年に甚大な土砂災害のあった那智川流域（和歌山県那智勝浦町）
のジオサイトや砂防堰堤を巡りながら、防災に関わる知識を深めようという
趣旨のイベントでした。
参加費１０００円で、４０名程度の参加者でした。


初めは、河川の氾濫により多くの被害が出た井関地区。
災害の怖さを忘れないための碑で、被害や状況の説明を受けました。
ここには当時の様子を伝える浸水深３．５５ｍを記したポールも立っています。
水流の凄まじさに思いを馳せつつ、参加者全員で黙祷を捧げました。


次は大きな土石流が発生した金谷山の崩壊地（源頭部）が望める場所に。

崩壊地付近には、上部に火成岩（花崗斑岩）、下部に堆積岩（熊野層群）の境界が
見えます。そこは、小さな滝になっていました。
この境界付近が大きな土石流の要因になっているのでは、と考えられています。
この付近では、学生時代の友人が研究していた玉ねぎの皮が向けるように、
割れていく花崗岩の球状風化や、
もっと過去の土石流で流れ、堆積した大きな石がたくさん見られました。

続いて、那智の滝に移動して、みんなで記念撮影。
那智の滝の麓近くでは、大正時代からの水力発電があるそうです。
先日の雨で水量も多く、迫力ある滝の様子に見入っていました。
那智の滝も、地質境界付近に位置し、滝となっている部分は
火成岩からなっているそうです。

大門坂の駐車場でお弁当を食べて尻剣谷に入りました。
ここも２３年の災害で土石流が発生した渓流です。

この渓流に分け入ると、



一度溶けて固まったような形の石や、人が掘ったと思われる穴、赤い土など
他のところとちがって、少し自然っぽくないものに出くわします。
というのも、那智地域では、昔から銅の採掘・精錬が行われていたからだそうです。
その名残が、落ちている石や地形に現れています。

さらに深く分け入ると、

石を積み上げてできた精錬所跡に出くわします。
熊野の産業の歴史の一端を垣間見ることができる貴重な場所です。

最後は、この渓流に作られた砂防堰堤を見学。

なかなか間近で見ることがない砂防堰堤。
鋼製のスリットで、大きな岩を止めることで土石流を止めることを狙ったものです。
おっきなジャングルジムみたいです。

近畿地方整備局の職員さんが丁寧に砂防堰堤の構造や工法、
効果や計画論を教えてくれました。
大人気で、質問攻めに遭われていました。
みなさん、砂防堰堤に関心が高いようでした。


前日の天候と打って変わって、とても穏やかで温かい一日でした。
普段は見えないところに入って、地形を詳しく見たり、自然の石を眺めたり
その違いに目を向けることで文化や歴史を感じることができました。